Rekurencja i fraktale

Rekurencja polega na rozwiązywaniu problemu w oparciu o rozwiązania tego samego problemu dla danych o mniejszym rozmiarze. Realizacja rekurencji w informatyce polega na tym, że dany program wywołuje samego siebie. Rekurencyjny zapis obliczeń jest zwykle bardziej przejrzysty. Przykładem zastosowania rekurencji są fraktale. Fraktal jest to obiekt ‘samo-podobny’. Jego części są podobne do całości. 

Rozważmy następujący fraktal. Dla n=1 jest to kwadrat. Długość boku kwadratu oznaczmy jako a.

Dla n=2 jest to kwadrat we wnętrzu powyższego kwadratu, obrócony o  45 stopni, którego długość boku wynosi $a \sqrt{2} \over {2}$, tak jak na rysunku ponizej:

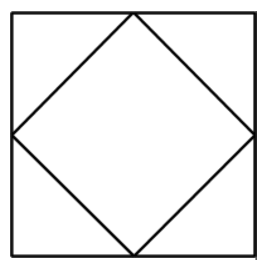
Łatwo domyślić się, jak wyglądają kolejne kroki. Przykład, dla n=10 znajduje się poniżej:

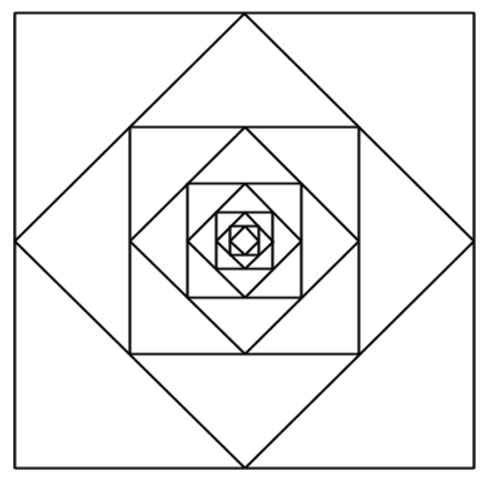
Twoim zadaniem jest obliczyć sumę obwodów kwadratów tworzących opisany fraktal dla n=50. Początkowa długość boku kwadratu to 137,89. Wynik podaj z dokładnością do 3 miejsc po przecinku.