Monte Carlo

Metoda Monte Carlo jest bardzo popularną metodą, która wykorzystuje losowość do rozwiązywania złożonych problemów. Znajduje zastosowanie w wielu dziedzinach, np. w obliczaniu objętości skomplikowanych brył, modelowaniu procesu zderzania się cząstek, szukaniu kształtu, jaki prawdopodobnie przyjmie w komórce łańcuch białkowy i wielu innych.

Metoda działa następująco: przyjmijmy, że chcemy obliczyć pole koła, które jest wpisane w kwadrat 2 x 2. Losujemy jakiś punkt z tego kwadratu i sprawdzamy czy leży w kole, czy poza nim. Zauważmy, że prawdopodobieństwo wylosowania punktu z koła wynosi dokładnie $\frac{P_{koła}}{P_{kwadratu}}$, a poza kołem: $1 - \frac{P_{koła}}{P_{kwadratu}}$. Powtarzamy tę procedurę możliwie dużo razy, np. milion. Spodziewamy się, że wśród wszystkich punktów mniej więcej $\frac{P_{koła}}{P_{kwadratu}}$ z nich wyląduje w środku koła, a $1 - \frac{P_{koła}}{P_{kwadratu}}$ poza kołem. Jeżeli więc z miliona punktów 200 000 znalazło się w kole wnioskujemy, że koło ma pole $$P_{kwadratu} * \frac{200000}{1000000} = 4 * \frac{1}{5} = 0.8$$ Im więcej punktów wylosujemy tym większą pewność będziemy mieli co do otrzymanego wyniku.

Poniżej znajduje się wykres funkcji danej wzorem:

$$y(x) = ( sin(\frac{x}{2}) * cos(x-2) + x^{\frac{1}{x}} ) ^2 $$ na przedziale (0, 20).

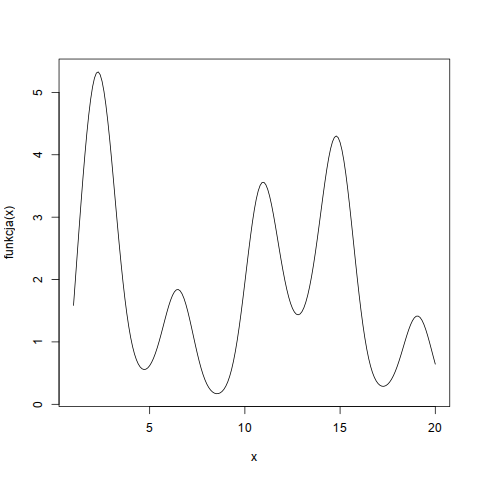
Twoim zadaniem jest policzenie pola pod wykresem tej funkcji korzystając z metody Monte Carlo. Wynik podaj w zaokrągleniu do liczb całkowitych.

Dobra rada: żeby uzyskać w miarę dokładny wynik, sugeruję losowanie co najmniej miliona punktów. Jeśli uznasz, że to za mało (bo spróbowałaś/eś kilka razy i uzyskane wyniki za mocno się różnią) zwiększ liczbę iteracji.