Model Isinga 2D
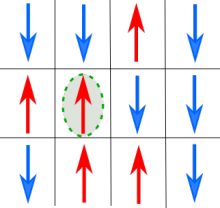
W zadaniu Model Isinga rozpatrywaliśmy cząstki ułożone w kole, jakby w spętlającej się przetrzeni jednowymiarowej. Tym razem cząstki znajdują się w przestrzeni dwuwymiarowej, każda ma więc czterech sąsiadów - na górze, na dole, z prawej i z lewej (po skosie nie). Załóżmy przy tym, że płaszczyzna, na której leżą cząstki jest spętlona, tak, jak poprzednio była spętlona prosta: to znaczy, że sąsiadami cząstek w pierwszym rzędzie są również te z ostatniego, cząstek w ostatniej kolumnie te z pierwszej etc. W ten sposób każda cząstka ma czterech sąsiadów. Energia cząstki zależy od spinów wszystkich czterech sąsiadów i jest sumą energii par: przykładowo, dla cząstki zaznaczonej na rysunku zielonym okręgiem, energia wynosi 2 * 5 (za dwóch sąsiadów o przeciwnym spinie) + 2 * 1 (za dwóch sąsiadów o zgodnym spinie) = 12. Energia układu to suma wszystkich takich energii.
Załóżmy, że mamy siatkę 10 x 10, na której znajdują się obdarzone spinem cząstki. Spiny części z nich są ustalone i nie mogą się zmieniać; ich spiny wpisane są w pliku ising_2d.txt. Pozostałe są oznaczone zerami i mogą zmieniać swój spin. Cząstki te będą chciały tak ustawić swój spin, żeby energia układu była jak najmniejsza. Jaką najmniejszą energię może im się udać uzyskać?
| Załącznik | Wielkość |
|---|---|
| 241 bajtów |
- Zaloguj się albo zarejestruj aby dodać rozwiązanie
-


